Black-Scholes Option valuation and Greek sensitivity analysis
Today we are valuing a simple, vanilla, option using Black-Scholes of course. I have attached the spreadsheet for you to run the val, there is no VBA element to this sheet- I removed the VBA calcs, it’s very simple though.
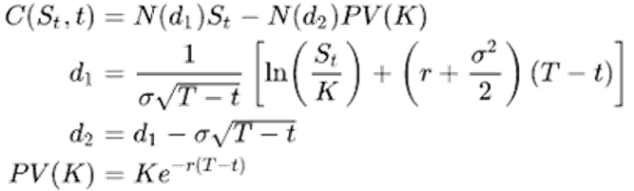
This time though, we will also be working through the main sensitivities.
I am sure you have learnt this in school so I will spare you the theory and perhaps go straight into the Greeks:
The Greeks in finance are risk sensitivities, so, how sensitive the price of a derivative, in this case an option, is to a change in an underlying parameter on which the value of the instrument is dependent. It will make more sense below, read on.
The purpose of this exercise is for you to visualise the purpose of each parameter and how changes in the price of the underlying (the share price) affect each of the parameters, we will be looking at the first-order Greeks: Delta, Vega, Theta, Rho and Lambda as well as Gamma, a second-order Greek.
Let's get into it:
Delta Δ
The rate of change of the option price with respect to the price of the underlying asset. It is the slope of the curve that relates the option price to the underlying asset price. Suppose that the delta of a call option on a stock is 0.6. This means that when the stock price changes by a small amount, the option price changes by about 60% of that amount (Hull, 2012). In general,
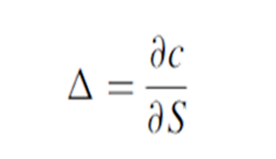
Gamma Γ
The gamma of a portfolio of options on an underlying asset is the rate of change of the portfolio’s delta with respect to the price of the underlying asset. It is the second partial derivative of the portfolio with respect to asset price (Hull, 2012):
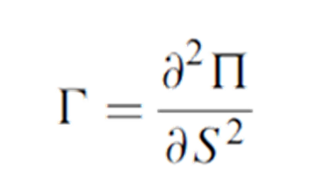
If gamma is small, delta changes slowly.
Vega v
The rate of change of the value of the portfolio with respect to the volatility of the underlying asset.
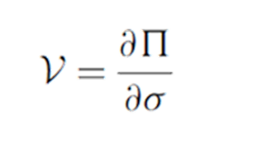
Theta Θ
The theta of a portfolio of options is the rate of change of the value of the portfolio with respect to the passage of time with all else remaining the same. This is time decay. For a European call option on a non-dividend-paying stock, it can be shown from the Black–Scholes–Merton formula that:
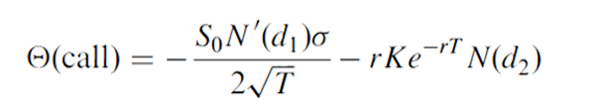
Where d_1 and d_2 are defined in the BSM equation and
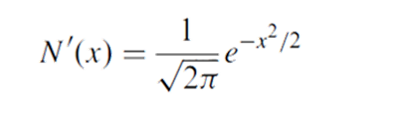
is the probability density function for a standard normal distribution.
For a European put option on the stock,
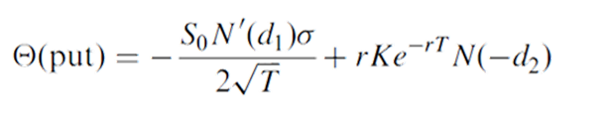
Because N(-d_2) = 1 – N(d_2), the theta of a put exceeds the theta of the corresponding call by rKe^-(rT)
Rho ρ
The rho of a portfolio of options is the rate of change of the value of the portfolio with respect to the interest rate:
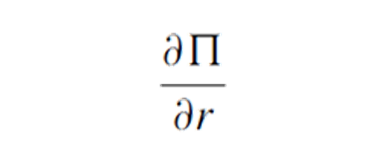
Lambda λ
Lambda λ, omega Ω, or elasticity, is the percentage change in option value per percentage change in the underlying price, a measure of leverage, sometimes called gearing.
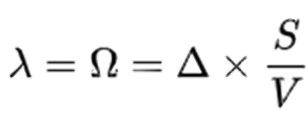
As a first approximation:
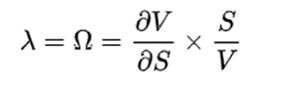
Download the spreadsheet here or click on the pic below :-).
Dont forget to get in touch:
@VumileSithebe on Twitter
Vumile Sithebe on LinkedIn













Comments